Stanford Coursera Machine Learning
Andrew Ng
- The heart of MATLAB is matrix.
- Default data type is double.
- Lambda:
g = arrayfun(@(x) 1/(1+exp(-x)), z);. - Mathematical operations use index starting from 1. And
X(1, :)is different fromX(1). A(:)is used for matrix unrolling to vector.theta'*thetais different fromtheta*theta'; thustheta .^2is preferred.dpquitto quit the debug mode.X(2:end, :): useendfor slicing.- Cell array is indexed by
A{1}. ~to skip a return value:[U, S, ~] = svd(Sigma).- Matrix multiplication orders depend on whether the data point is a col vector or row vector.
- For loop:
for epsilon = min(pval):stepsize:max(pval)
- Cost function for one var
- Gradient descent for one var
- Feature normalization
- Cost function for multi-var
- Gradient descent for multi-var
- Normal Equations
- Sigmoid function
- Cost function for logistic regression (LR)
- Gradient descent for LR
- Predict function (hypothesis)
- Cost function for regularized LR
- Gradient descent for regularized LR
}{\partial \theta_j} = \Bigg(\frac{1}{m}\sum_{i=1}^m{\big(h_\theta(x^{(i)})-y^{(i)}\big)x_j^{(i)}}\Bigg)+\frac{\lambda}{m}\theta_j)
- Regularized Logistic Regression
- One-vs-all classifier training
- One-vs-all classifier prediction
- Neural Network predict function
}{\partial \theta} = \frac{1}{m}X^T\big(h_\theta(X)-y\big)+\frac{\lambda}{m}\theta)
- Feedforward and cost function
- Regularized cost function
- Sigmoid gradient
- Neural Net gradient function (Backpropagation)
- Regularized gradient
=\\frac{1}{m}\\sum_{i=1}^{m}\\sum_{k=1}^K{{\\big[-y_k^{(i)}\\log{(h_\\theta(x^{(i)}))_k}-(1-y_k^{(i)})\\log{(1-h_\\theta(x^{(i)}))_k}\\big]}}+\\frac{\\lambda}{2m}\\sum_{l}{\\sum_{j\\in (l+1)}{\sum_{k\in l}{(\Theta_{j,k}^{(l)})^2}}})
}= (\Theta^{(l)})^T\delta^{(l+1)}\circ g'(z^{(l)}))
}}J(\Theta)=D_{ij}^{(l)}=\frac{1}{m}\Delta_{ij}^{(l)}+\frac{\lambda}{m}\Theta_{ij}^{(l)})
- Regularized LR, cost function (review)
- Regularized LR, gradient (review)
- Learning Curve - Bias-Variance trade-off
- Polynomial feature mapping
- Cross validation curve - (select lambda)
=\\theta_0+\\theta_1 x_1+...+\theta_p x_p), where x_i = normalize(x .^ i)
- Gaussian Kernel
- Parameters (C, sigma)
- Email preprocessing
- Email feature extraction
}cost_1{(\theta^Tx^{(i)})}+(1-y^{(i)})cost_0{(\theta^Tx^{(i)})}\big]}+\frac{1}{2}\sum_{j=1}^n{\theta_j^2})
}, x^{(j)})=\exp{\Bigg(-\frac{||x^{(i)}-x^{(j)}||^2}{2\sigma^2}\Bigg)})
}cost_1{(\theta^Tf^{(i)})}+(1-y^{(i)})cost_0{(\theta^Tf^{(i)})}\big]}+\frac{1}{2}\sum_{j=1}^n{\theta_j^2})
} = K(x^{(i)}, l^{(k)}))
- Find closest centroids
- Compute centroid means
- PCA
- Project data
- Recover data
}:= \operatornamewithlimits{argmin}_{j} ||x^{(i)}-\mu_j||^2)
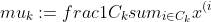}})
- Estimate Gaussian parameters
- Select threshold
- Collaborative Filtering cost
- Collaborative Filtering gradient
- Regularized cost
- Gradient with regularization
}}=\sum_{j:r(i,j)=1}{\big((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\big)\theta_k^{(j)}}+\lambda x_k^{(i)})
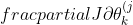}}=\sum_{i:r(i,j)=1}{\big((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\big)x_k^{(i)}}+\lambda \theta_k^{(j)})
