Functionally Reduced And-Inverter Graph (FRAIG)

Purpose

This program is an electronic design automation (EDA) tool written in C++. It can reduce the complexity (i.e., number of logic gates) of Boolean circuits automatically without changing the functionality of the circuit. In other words, given an existing Boolean circuit, it can build an equivalent circuit with fewer gates.

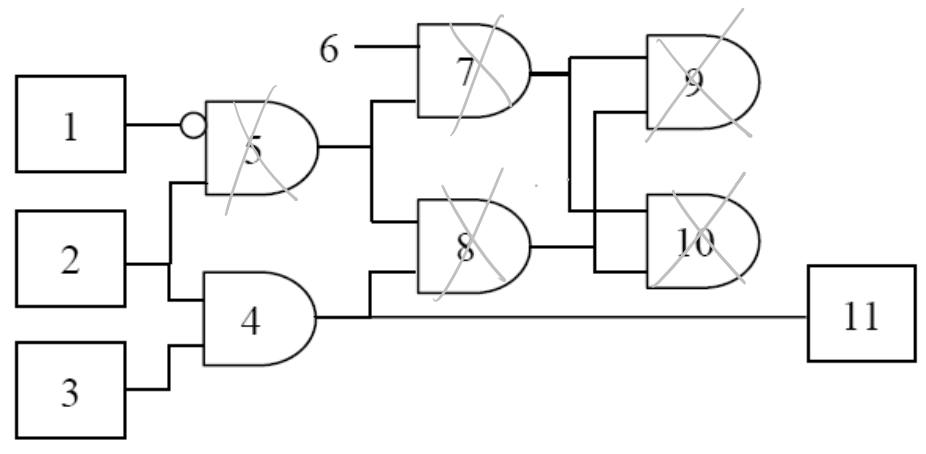
A trivial example is illustrated in the picture below. In the picture, rectangles are the primary inputs and outputs of the Boolean circuit, semi-ovals are AND gates, the small circle is an inverter, and the lines are the connections between logic gates. By inputting Boolean patterns to the primary inputs (i.e., gate 1, 2, and 3) the primary output (i.e., gate 11) should output Boolean patterns according to the Boolean function of this circuit. However, if we remove gate 5, 7, 8, 9, and 10, the input-output relation of this circuit (i.e., the function of this circuit) is unchanged. The purpose of this program is to perform circuit simplification like this (though it can handle much larger and non-trivial cases). In the real world, such optimization can reduce the area, timing, and power consumption of the circuits.

Supported Operations

The following summarizes the supported operations of this program. For a detailed description, please refer to this.

Supported operations include:

1. CIRRead: Reads in a circuit from an ASCII AIG file (.aag) and constructs the circuit netlist within the program
2. CIRPrint: Prints the circuit netlist
3. CIRGate: Reports a gate
4. CIRWrite: Writes the netlist to an ASCII AIG file
5. CIRSWeep: Removes the gates that cannot be reached from primary outputs of the circuit
   • Relevant data structure and algorithm: Depth-First Search
   • In the example in the picture below, gate 5, 7, 8, 9, and 10 cannot be reached from the primary output (gate 11). These gates can be removed without changing the function of the circuit
     • 
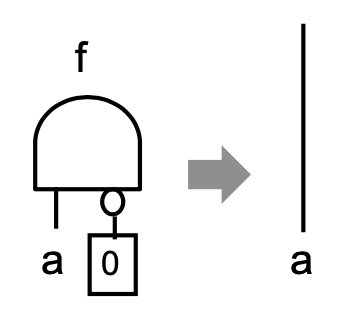
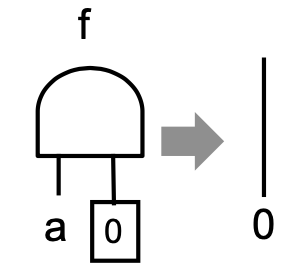
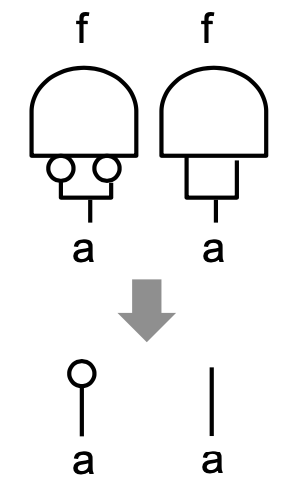
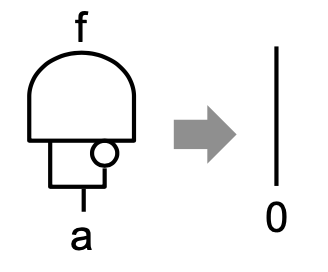
6. CIROPTimize: Performs trivial optimizations. Some examples of trivial circuit optimization are illustrated in the pictures below
   • Relevant data structure and algorithm: Depth-First Search
   • Input has constant 1 ==> Replaced by the other input
     • 
   • Input has constant 0 ==> Replaced with 0
     • 
   • Identical inputs ==> Replaced with the (input + phase)
     • 
   • Inverted inputs ==> Replaced with 0
     • 
7. CIRSTRash: Performs structural hash on the circuit netlist
   • Relevant data structure and algorithm: Hash table, Depth-First Search
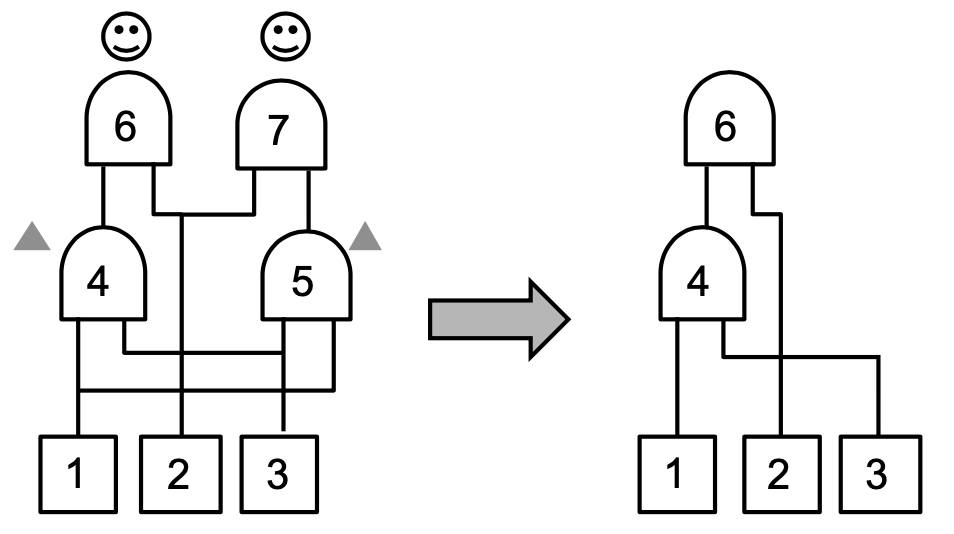
   • In the example below, gate 4 and 5 in the original circuit are both connected to gate 1 and 3. Their functions are thus identical so can be merged into a single gate. After gate 4 and 5 are merged, gate 6 and 7 becomes identical due to the same reason and can also be merged
   
8. CIRSIMulate: Generates random Boolean pattern at the primary inputs (or read pre-defined patterns), performs Boolean logic simulation on the circuit, and records the output pattern of each gate
   • Relevant data structure and algorithm: Hash table, Depth-First Search
   • The purpose of the simulation is to identify logic gates that are functionally identical and therefore can be merged
   • If a pair of logic gates are functionally identical, the output pattern of these two gates must be the same during the entire simulation process (but not necessary the other way around)
   • The program scans through all the simulated output patterns of each logic gate and partitions the gates into groups of gates that are potentially functionally identical (called Functionally Equivalent Candidate Groups). Any two gates if the circuit will be in the same Functionally Equivalent Candidate Group if and only if they have identical simulated output pattern. If the output pattern of a gate is not identical to any other gate, it should be in a Functionally Equivalent Candidate Group containing only itself.
9. CIRFraig: Performs FRAIG operation on the circuit
   • Relevant data structure and algorithm: SAT problem
   • Note that gates within the same Functionally Equivalent Candidate Group have identical output patterns during the simulation and are therefore potentially functionally identical. However, it is not guaranteed. We need formal verification to tell whether any two of the gates in the Functionally Equivalent Candidate Group are truly functionally identical. This verification problem can actually be transformed into a SAT problem
   • We use the MiniSat library to perform such verification
   • When the FRAIG operation is performed, the program scans through each Functionally Equivalent Candidate Group and uses SAT solver to tell if any two of the gates in the Functionally Equivalent Candidate Group are functionally identical. If yes, the program will merge the pair of gates, further simplifying the circuit

Supported Platform

Linux / Ubuntu 5.4.0-6 ubuntu1~16.04.4
Mac / Homebrew GCC 7.2.0

How to execute

For Linux

make linux
make
./fraig

For Mac

make mac
make
./fraig

The lines above initiate the program. For detailed instructions on how to use the program to perform circuit simplification, please refer to this.

Credit

This project is designed and guided by professor Chung-Yang (Ric) Huang at National Taiwan University.